Table of Contents
Conflicting Principles
Pareto-optimal solutions
Each principle describes a certain aspect of the problem. For example KISS is about the value of simplicity. A solution is better when it is simpler. Another principle that might also be considered in the same context is GP which says that a more generic solution is better than a specific one, as it can be applied to a broader set of problems which increases reusability.
This is a typical example of two conflicting principles. Both are valid. A solution is better (wrt. ease of writing, ease of use, readability and potential for fault introduction) when it is simpler. And a solution is better (wrt. reusability and changeability) when it is more general. These principles are conflicting. A solution normally is either simple or generally applicable but not both. As the aspects, the principles refer to, are typically not binary, adherence to the principles can be informally rated on a gradual scale. A good design decision will now balance these principles and come up with a compromise that is generalized to some extend but not too much in order to keep the solution reasonably simple.
While typically there is no solution which is good in every aspect or principle (e.g. which is totally simple and totally generic) there might be solutions that are bad in both aspects/principles (e. g. ones which are neither simple nor generally applicable). So a good solution is Pareto-optimal, which means there is no other solution which is better in one aspect/principle while being at least equally good in all others.
In that way good solutions can be distinguished from bad ones. Nevertheless there can be several good, i.e. Pareto-optimal, solutions. For choosing between them, it is necessary to make a judgment which aspect is more important. When readability is more important, the simpler solution should be chosen and in case of reusability being more important the generic one should be chosen. This is either a choice of requirements or (if the requirements are not clear about that) personal style.
Example
A trivial example that shows the idea could be a square root function. In a program that needs the square root of 2, the following design problem could arise: What is the best way to compute the square root of 2? There are several possible solutions:
- A constant:
sqrt_2 = 1.4142135623730951 - A method that computes the square root of 2:
double sqrt_2() - A method that computes arbitrary real square roots of real numbers:
double sqrt(double radicand) - A method that computes arbitrary real powers to real numbers:
double power(double base, double exponent) - A method that computes arbitrary complex powers to complex numbers to an arbitrary precision:
BigComplex power(BigComplex base, BigComplex exponent, BigDecimal epsilon)
The following figure depicts the solution space of the problem:
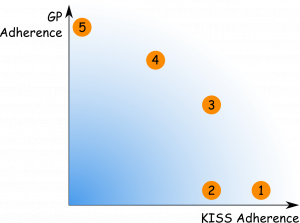
Possible solutions lie in the blue area. If it existed, an optimal solution with respect to both principles, KISS and GP, would be shown in the top right corner. And an overly complex solution which is not general at all would be near the origin. The above solutions are numbered in the graphic. Note that this is just an informal rating which can be done quickly and doesn’t involve complex metrics.
Each solution has its advantages and disadvantages. Solution 1 is the easiest. It is simple to implement and easy to read. On the other hand it is very specific and can only be reused when exactly the same value is needed. This is the solution that follows KISS to the greatest extend.
In contrast to that, solution 5 is very generic and can be applied to a broad set of problems. So it can be reused in many other contexts. The downside is that it is difficult to write and difficult to use. These are the both extremes when one principle is almost neglected.
Solution 2 represents a bad solution. It is certainly more complex than 1 but does not provide a more general solution. And it is also less general than 3 but is not simpler.
The solutions that are commonly implemented in standard math libraries are 3 and 4. They represent a compromise between simplicity and general applicability. Neither is better than the other. 4 is more complex but also more powerful. They both represent Pareto-optimal solutions.
And even solutions 1 and 5 are Pareto-optimal. They may be less common but one could think of situations when they might be preferred over the others. There may be a case when the square root of 2 is the only root necessary and a math library containing a square root function may not be available due to limited memory on a special purpose hardware. Or there may be complex numbers necessary for a certain scientific computation.
This approach does not tell which of the four good solutions should be chosen (only solution 2 is sorted out). It is more a way of thinking than a general method. Rating solutions with real numbers or even visualizing the solution space graphically (like in the figure above) is not necessary and in most cases also not helpful. But stating that the design decision to make is a question of simplicity versus general applicability is a valuable statement which helps the designer to find an appropriate solution. The approach is about exploring the dimensions of the solution space to a given design problem and the wiki describes the relationships between the principles, i.e. the dimensions of the design space.
